Recientemente, Alva Majo, desarrollador de videojuegos indie y youtuber, publicó un vídeo donde explicaba cómo creó Alvabot, un sintetizador de habla que utilizaba muestras de su propia voz. Como, además, hizo público el código fuente y las muestras de voz, decidí que podía ser divertido intentar llevarlo un poco más allá y hacer que cantase. ¡Y lo he conseguido!
Sí, vale… el resultado no es exactamente profesional, pero para ser algo hecho en un par de días, creo que no está mal.
El código y las muestras de cantabot están disponibles en mi repositorio GIT bajo una licencia MIT/Expat (que viene a ser equivalente al «haz lo que te de la gana» con la que distribuyó Alva Majo su código original). También están disponibles las pequeñas utilidades que usé para reconstruir las muestras y adaptarlas para la tarea.
El proceso fue algo alambicado, pero al final no tiene mucha ciencia. Obviamente, si hubiese querido conseguir mejores resultados tendría que haber utilizado otras técnicas, pero la idea era hacer sólo un pequeño divertimento.
En primer lugar escribí una pequeña herramienta en Python (analizador.py, disponible en el repositorio) que me permite ver la forma de onda de un fichero WAV, escoger un trozo entre dos puntos concretos, calcular la frecuencia de dicha onda, y cortar entre los máximos de dicho trozo (todo esto lo explicaré mejor a continuación). Gracias a que Python tiene módulos para todo, no necesité programar casi nada, sino que ha sido más una operación «de pegar cosas».
Así, tomé los samples de las vocales y utilicé la herramienta anterior para revisar la forma de onda de cada una (en este artículo denominaré sample a cada fichero de audio con el sonido de una vocal o una consonante; y utilizaré el término muestra para referirme a cada uno de los datos de sonido que hay dentro de cada fichero; esto es: cada «número» dentro del fichero .WAV será una muestra).
Aquí vemos una ampliación de la vocal A, tal y como se ve en la herramienta:
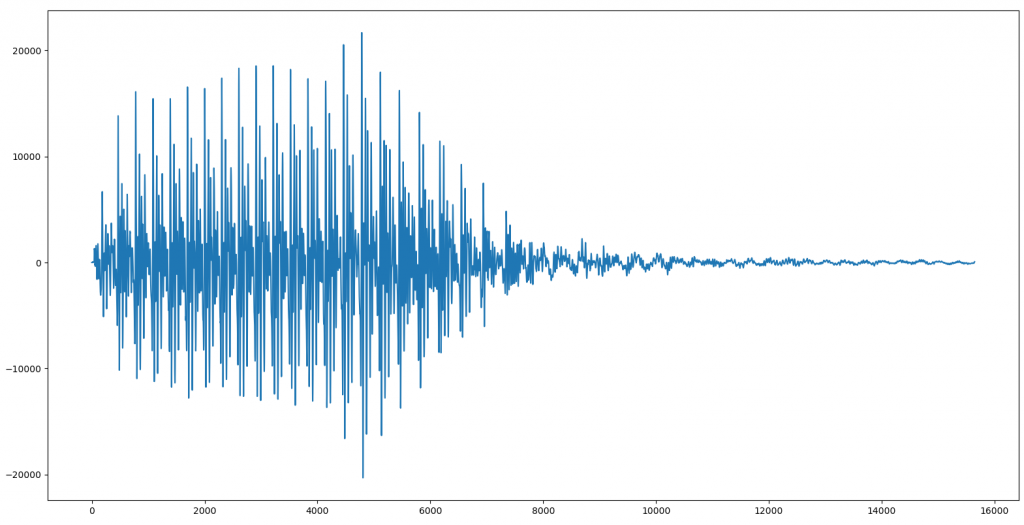
Si nos fijamos, vemos que parece que hay cierta «repetición». O sea: la onda no es «aleatoria», sino que parece que hay un bloque que se repite en el tiempo (como se puede apreciar por esos picos espaciados de manera regular). Es verdad que la amplitud (la altura) no es constante, pero eso es simplemente porque Alva es un ser humano, y por mucho empeño que ponga es imposible que mantenga exactamente la misma intensidad durante toda la vocal, sino que inevitablemente subirá y bajará un poco en el tiempo.
Para verlo mejor, ampliemos un trozo:
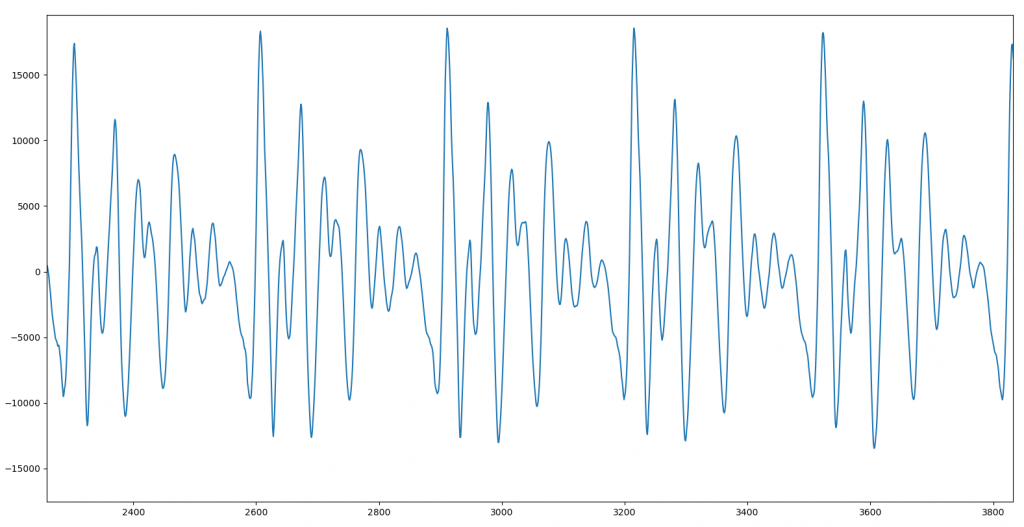
Aquí ya se ve mucho mejor cómo la vocal es, en realidad, un trocito de sonido que se repite una y otra vez. En esta imagen concreta lo vemos repetido cinco veces. Esto significa que si creamos un sample con sólo ese trozo, podremos repetirlo en bucle y conseguir que el ordenador pronuncie una vocal durante todo el tiempo que queramos, sin que se noten cortes, ligaduras ni nada por el estilo. Esto es fundamental a la hora de cantar porque cada nota puede tener una duración diferente a las demás, y son justo las vocales las que se «estiran» en el tiempo para cubrir todo el tiempo que dura una nota.
Aquí es donde mi herramienta analiza.py me pide dos puntos en la gráfica. El primero tiene que estar un poco ANTES de uno de los máximos, y el segundo un poco DESPUÉS del siguiente máximo. Entonces, la herramienta busca hacia adelante el valor máximo local desde el primer punto, y hacia atrás desde el segundo punto, para así recortar con precisión el trozo periódico. Para la vocal A utilicé 1668 y 2023, marcados en rojo en la imagen, y que como vemos caen justo cerca de dos máximos consecutivos. El propio programa busca los máximos, los cuales están en 1697 y 2001.
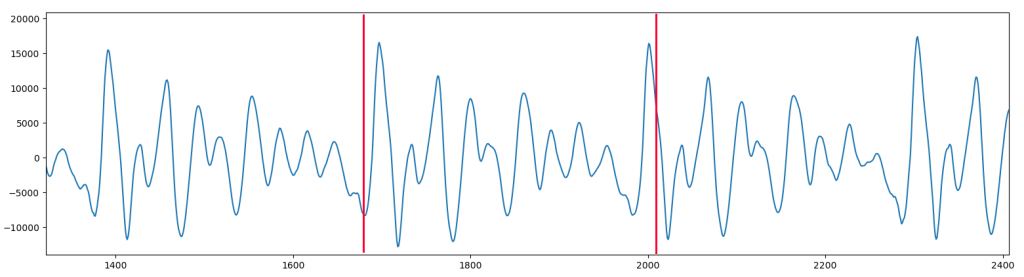
Lo segundo que hice fue calcular la frecuencia fundamental de cada vocal. Para los que no sepan a qué me refiero, la frecuencia fundamental determina la «nota» en la que está sonando la vocal. Cuando mayor sea la frecuencia, más alta en la escala será la nota. Al principio hice algunas pruebas con la transformada de Fourier, hasta que me di cuenta de que no necesitaba complicarlo tanto, pues simplemente con saber el número de muestras que hay en el «trozo» repetitivo y la frecuencia de muestreo, ya puedo obtener la frecuencia fundamental del sample.
Así, por ejemplo, si decidimos utilizar para la vocal A el bloque situado entre los picos de las muestras 1697 y 2001, vemos que hay un total de 304 muestras en él, lo que significa que si dividimos la frecuencia de muestreo de este fichero .WAV (que es de 44100 muestras/segundo) entre dicho valor, nos dará que la frecuencia a la que Alva pronunció la letra A es de 145 Hz.
Repitiendo este proceso para las cinco vocales, sale que cada una fue pronunciada con estas frecuencias:
vocal A: muestras 1697 a 2001, 145 Hz
vocal E: muestras 555 a 855, 147 Hz
vocal I: muestras 2968 a 3242, 161 Hz
vocal O: muestras 2246 a 2544, 148 Hz
vocal U: muestras 3027 a 3317, 152 Hz
Esto demuestra que Alva Majo NO es un robot, pues no es capaz de afinar correctamente. Por eso cada vocal tiene una frecuencia diferente.
Pero claro, para nosotros esto es un problema porque si queremos que el ordenador cante, necesitamos que las muestras estén todas en la misma frecuencia. Si no, lo único que conseguiremos es un ordenador que desafina.
Afortunadamente, una vez que tenemos ya aislado el bloque periódico de cada vocal, ajustar su frecuencia es muy sencillo: sólo necesitamos hacer que todas midan lo mismo (pues la frecuencia fundamental depende del tamaño del bloque y de la frecuencia de muestreo; como la frecuencia de muestreo tiene que ser la misma para todos los samples, tenemos que conseguir que el número de muestras sea igual). Si calculamos la media de todas esas frecuencias, nos salen 150 Hz, así que ajustaremos todas a ese valor para evitar tener que desplazarlas demasiado. Y si ahora dividimos la tasa de muestreo entre esa cifra, nos sale que cada bloque debe tener 44100/150 = 294 muestras. Por supuesto, no se trata de añadir, por ejemplo, ceros al final, porque entonces estaríamos modificando la señal. Lo que necesitamos es «inventarnos» muestras en medio para estirarla si es demasiado corta, o «tirar a la basura» muestras si es demasiado larga. Por supuesto, si añadimos muestras éstas deben «encajar» con las que las rodean; y si quitamos muestras, debemos hacerlo de manera «repartida». Esto, como no, tiene un nombre: remuestreo o cambio de tasa de muestreo, y el módulo scipy incluye una función llamada resample() que lo hace. Así que en la parte final de la herramienta hago una llamada a dicha función para ajustar cada sample justo antes de grabarlo en disco.
Para poder evaluar los resultados, podemos comparar el antes:
con el después:
Ahora llega el momento de hacer lo mismo con las consonantes, pero esto es un poco más complicado, pues éstas no tienen por qué tener un patrón (aunque algunas sí), por lo que será difícil calcular su frecuencia… o no, porque, afortunadamente, Alva grabó todas las consonantes seguidas de todas las vocales. No tenemos sólo el fonema ‘P’, sino que también tenemos los sonidos de ‘PA’, ‘PE’, ‘PI’, ‘PO’ y ‘PU’, así que podemos medir la frecuencia a la que pronunció la vocal y asumir que es la misma que la del fonema de la consonante. Luego sólo tendremos que cortar justo en el punto donde termina la consonante y empieza la vocal, y tendremos el sonido puro de la consonante. Veamos un ejemplo con la sílaba «DA»:
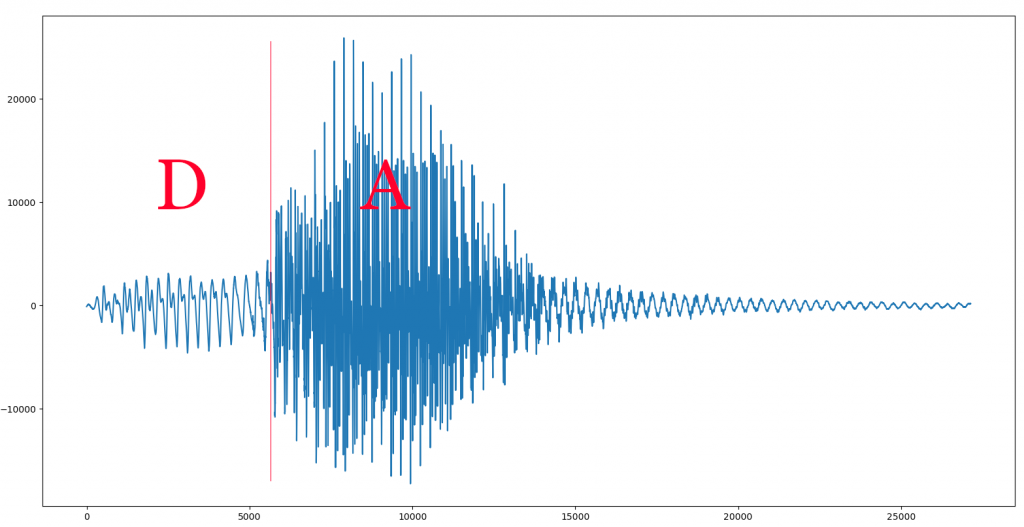
Para hacer esto escribí otra pequeña herramienta, cortar_consonantes.py, la cual carga un fichero .WAV, muestra su forma de onda para que podamos buscar dos muestras que delimiten un periodo de la vocal, y nos pide que tecleemos su posición. Con ellas calcula la frecuencia a la que está pronunciada y también cuanto tiene que estirar o encoger todo el fichero WAV para ajustarlo a los 150 Hz que decidimos que sería nuestra frecuencia central.
Una vez que está ajustada, nos pide el número de muestra en la que realizar el corte para separar la consonante de la vocal. Como no es fácil acertar, lo que hice es que, tras dar un punto de corte, reproduzca la consonante seguida de la vocal «I» (para lo cual, utilizo los samples que generé antes). De esta manera, si se recorta demasiado poco y se cuela parte de la vocal original, sonará AIIIIIII en lugar de IIIIIII. Así podremos ir ajustando hasta encontrar el punto óptimo de cada consonante. Cuando hayamos encontrado el punto exacto, simplemente pulsamos RETURN en lugar de meter un nuevo número y el programa grabará el nuevo sample con sólo la consonante, ya ajustada a 150 Hz.
Algunas consonantes, pese a todo, son sonoras, lo que significa que SI están formadas por una zona repetitiva. En concreto, para la B, la M y la N utilicé el mismo sistema que para las vocales, pues se entendían mucho mejor que extrayéndolas «tal cual» de los samples.
Haciendo que hable
Ahora que ya tenemos los sonidos vocales y consonantes aislados y a la misma frecuencia, podemos hacer una primera prueba que se limite a hablar. Para ello escribí hablar.py, que generará un fichero habla.wav en el que pronunciará la frase que se le pase por la propia línea de comandos.
Lo primero que hace este programa es sustituir las letras por fonemas, de manera que no hace falta pensar en sonidos sino que podemos escribir directamente una frase. Además, si alguna vocal tiene tilde la pronunciará a una frecuencia ligeramente superior, lo que permite simular la entonación de las frases. En teoría se podría hacer que fuese completamente automático, y que si una palabra no tiene tilde, compruebe si acaba en n, s o vocal y, en base a ello, determine si es aguda o llana y ponga la tilde automáticamente, pero no me apeteció ponerme con ello, así que hay que hacerlo a mano.
Ejemplo: «Hóla, sóy cantabót hablándo.»
Y haciendo que cante
Y por último, está la herramienta final, cantar.py, que genera un fichero .WAV con una canción generada con las muestras.
El programa se compone de una clase con dos métodos fundamentales: interpreta() y pausa(). Estos dos métodos se deben ir llamando para introducir la partitura y la letra de la canción. Cada llamada renderiza los sonidos correspondientes, que se van añadiendo a un buffer interno. Cuando la canción está lista, se llama al método grabar(), que lo almacenará en disco en formato WAV con el nombre canta.wav.
El método pausa es el más sencillo, y simplemente recibe como parámetro un número decimal con el número de segundos de silencio que se deben añadir al buffer. Permite añadir silencios entre notas.
El método interpreta es el más complejo, y recibe tres parámetros:
- Un entero con la octava de la nota a interpretar. Este valor estará entre 0 y 12 e indica el semitono concreto. La correspondencia exacta está en el código fuente
- Un valor decimal con la duración en segundos de la nota.
- Un string con los fonemas a cantar en dicha nota
Para simplificar la composición, se definen seis variables (redonda, redondadot, blanca, blancadot, negra y negradot) con las duraciones en segundos. Se establece la duración de la redonda en 1,5 segundos, y el valor de la blanca y la negra queda definido automáticamente como la mitad y la cuarta parte de la redonda. A mayores, las duraciones con «dot» son un 50% más que la correspondiente sin «dot». Además, se definen también las variables nota_XX, con el valor de semitono correspondiente a cada nota (por ejemplo, nota_sol vale 5).
Por otro lado, a la hora de decidir cuanto tiempo dura cada fonema de la nota se siguen las siguientes reglas:
- Las consonantes durarán lo que dure su sample, salvo las consonantes «sonoras», que durarán 0,2 segundos
- Las vocales que no sean la última durarán 0,15 segundos
- La última vocal durará el tiempo necesario para completar la duración de la nota
Así, la última vocal durará realmente la duración de la nota menos la duración del resto de fonemas. Este valor se calcula automáticamente, lo que simplifica mucho meter una partitura.
Dado que ya nos preocupamos antes de ajustar todos los samples para que estuviesen a 150 Hz, ahora lo único que tenemos que hacer es ajustar la frecuencia de todos los fonemas a la necesaria para la nota. Y lo interesante es que para saber cuanto tenemos que ajustar la frecuencia, sólo necesitamos elevar la raíz doceava de 2 al valor del semitono que le pasamos a la función (por supuesto, tras restar 5, pues por convenio he decidido que los samples estarán en SOL).
¿Y por qué la raíz doceava de 2? En este vídeo de Minute Physics lo explican muy bien, pero para simplificar: como la frecuencia de una nota cualquiera tiene que ser la mitad de la frecuencia de la misma nota en la siguiente octava, y cada octava son doce semitonos, la única manera de que esto encaje es que la frecuencia de cada semitono sea la frecuencia del semitono anterior multiplicado por la raíz doceava de dos. Así que si quiero hacer sonar un LA (semitono 7 como vemos en la tabla de arriba), necesito subir la frecuencia de los fonemas en dos semitonos, o sea, multiplicar dos veces por la raíz doceava de dos. En cambio, si quiero interpretar un MI, tengo que bajar la frecuencia en tres semitonos; o sea, dividir tres veces entre la raíz doceava de dos.
¿Y cómo cambiamos la frecuencia de los fonemas? Pues exactamente como vimos antes: interpolando para estirarlos o encogerlos. Si los estiramos, la frecuencia baja; y si los encojemos, la frecuencia sube. Por tanto, una vez hemos calculado el factor entre la frecuencia inicial y la final, sólo tenemos que coger el número de muestras que tiene cada fonema y multiplicarlo por dicho factor, obteniendo así el nuevo número de muestras que tiene que tener. Con ese número llamamos a interpolate() para que haga su magia, y añadimos las muestras al buffer.
![]() Daisy, Daisy… por A cuadros está licenciado bajo una Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
Daisy, Daisy… por A cuadros está licenciado bajo una Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.